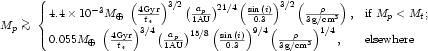A Hand-Waving Derivation of Planethood
by Hal Levison
The IAU recently defined a planet as any object large enough to clear
its neighborhood of small bodies. I have been asked if there is a
simple way to determine whether an object is a planet based on its
mass and its location within the Solar System. In general, the answer
is no, because it depends on the details of what its neighboring
planets are like and the dynamical state of the small bodies.
However, being a good theorist, I will not let reality stop me.
Indeed, it is possible to develop a back-of-the-envelope argument
based on a system containing the Sun and a planet of mass
Mp orbiting at a distance of
ap. The pieces of this argument have already been
developed for a different reason - the understanding of Oort cloud
formation. Thus, much of what I say here can be found in Tremaine
(1993. 'The distribution of comets around stars', ASP Conf. Ser. 36:
Planets Around Pulsars 36, 335-344).
In this simple system, there are two ways in which a planet can remove
a population of small bodies: 1) It can accrete all of them, or 2) It
can gravitationally eject them from the Solar System. I will treat
each of these separately.
- Ejection: As a small body gravitationally interacts with
a planet, it undergoes a random walk in orbital energy. A planet can
eject a small body if it is able to change the body's orbital energy
by an amount at least equal to its original value. Tremaine (1993)
shows that this occurs if
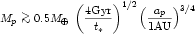
- Accretion: The probability that a small body will hit a
planet each orbit is
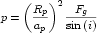 , where
Rp is the radius of the planet, Fg
is that classical gravitational focusing factor, and i is the
typical inclination of a small body. The gravitational focusing
factor is given by
, where
Rp is the radius of the planet, Fg
is that classical gravitational focusing factor, and i is the
typical inclination of a small body. The gravitational focusing
factor is given by 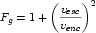 , where venc is the typical velocity of
an enounter between the small objects and the planet and
vesc is the planet's escape velocity. There is a
transistion in behavior when venc ~
vesc. This transition is a function of the mass of
the planet (through vesc) and its orbit (through
venc). In particular, I can define a tranition mass
(Mt) as:
, where venc is the typical velocity of
an enounter between the small objects and the planet and
vesc is the planet's escape velocity. There is a
transistion in behavior when venc ~
vesc. This transition is a function of the mass of
the planet (through vesc) and its orbit (through
venc). In particular, I can define a tranition mass
(Mt) as: 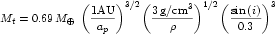 . If
Mp>Mt then gravitational focusing is
important.
Assuming that the small body has the same semi-major axis as the
planet, we can show that for a planet to accrete all the nearby small
bodies in the age of the Solar System (t*) it mass
must be:
. If
Mp>Mt then gravitational focusing is
important.
Assuming that the small body has the same semi-major axis as the
planet, we can show that for a planet to accrete all the nearby small
bodies in the age of the Solar System (t*) it mass
must be:
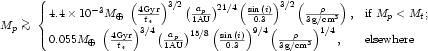
Putting it all together, we find:
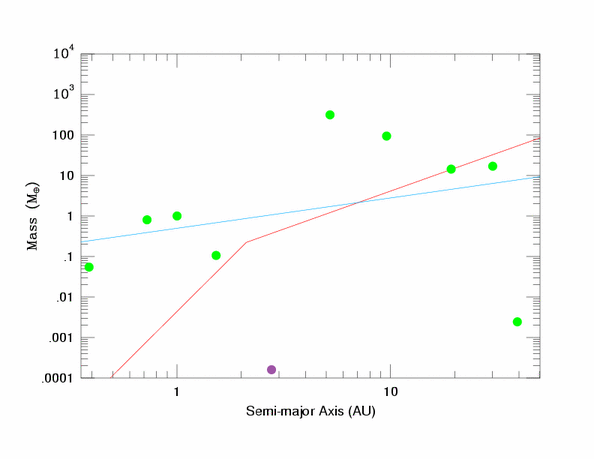
The green dots are the 9 'classical' planets. The purple shows Ceres.
Anything above the red line will accrete the small bodies in its
neighborhood, while anything above the blue curve will eject them.
The way to read this plot is that if an object is above
either line it is a planet. Therefore, there are 8 planets.
A Romanian translation of this page can be found here
Last modified 8/24/06.
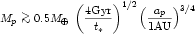
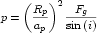 , where
Rp is the radius of the planet, Fg
is that classical gravitational focusing factor, and i is the
typical inclination of a small body. The gravitational focusing
factor is given by
, where
Rp is the radius of the planet, Fg
is that classical gravitational focusing factor, and i is the
typical inclination of a small body. The gravitational focusing
factor is given by 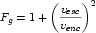 , where venc is the typical velocity of
an enounter between the small objects and the planet and
vesc is the planet's escape velocity. There is a
transistion in behavior when venc ~
vesc. This transition is a function of the mass of
the planet (through vesc) and its orbit (through
venc). In particular, I can define a tranition mass
(Mt) as:
, where venc is the typical velocity of
an enounter between the small objects and the planet and
vesc is the planet's escape velocity. There is a
transistion in behavior when venc ~
vesc. This transition is a function of the mass of
the planet (through vesc) and its orbit (through
venc). In particular, I can define a tranition mass
(Mt) as: 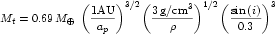 .
.