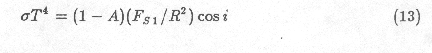CHAPTER 8 THERMAL ICE SEGREGATION

Most of the rest of this dissertation is concerned with the possibility that the Galilean satellites may have `checkerboard' surfaces, with icy and non-icy components spatially segregated. I was motivated in this investigation by the apparent presence of thermal contrasts on Ganymede that are not due to topography, as described in previous chapters. Another motivation was the search for a way of stabilizing the spectroscopically-inferred low latitude ice on Callisto, when previous theoretical studies had implied very rapid poleward migration for dark equatorial ice.
In this chapter I consider a plausible mechanism for producing a segregated surface on initially homogeneous dirty ice, and deduce timescales for the mechanism. In subsequent chapters I consider other processes that compete in determining the distribution of ice on the Galilean satellites, and investigate the spectroscopic evidence for ice abundance and distribution.

Introduction

It has been argued, for instance by Squyres (1980), that the great geological age of the surface units on at least Ganymede and Callisto implies that impact gardening will have thoroughly mixed the ice and non-ice components of the surface. Clark's (1980) interpretation of the near-infrared reflectance spectra of the three objects appears to support the view of a homogeneous surface, with a (minor) non-ice component intimately mixed with the ice. However, Seiveka and Johnson (1982) and Spencer and Maloney (1984) argue for segregated, bright ice on Callisto in order to explain the lack of massive poleward ice migration on that object. Purves and Pilcher (1980) and Shaya and Pilcher (1984) implicitly assume a segregated-ice surface in their models of ice migration on Ganymede and the other satellites. And the IRIS spectrum slopes on Ganymede, discussed in previous chapters, may be best explained by a laterally inhomogenoeus surface, perhaps of bright cold ice and darker, warmer, non-ice.
Is it possible to maintain segregated surfaces on the icy Galilean satellites in the face of the homogenizing effects of meteorite gardening One possible way, suggested by Spencer and Maloney (1984), is a positive feedback mechanism in which regions that are ice-rich will tend to be brighter and hence cooler than their surroundings, and will thus act as cold traps for the accumulation of more ice. A similar process for trapping of SO₂ on Io has been proposed by Fanale et al (1982). This chapter describes an attempt to quantify the cold-trapping model in order to determine the possible importance of the mechanism.

The Segregation Mechanism

The principles of the proposed segregation model are simple, and are illustrated in Figure 30. The icy Galilean satellites have surfaces composed of a mixture of ice and a darkening contaminant, presumed for present purposes to be initially in the form of small embedded particles, well mixed with the ice, as might result from a fresh meteorite impact. Variations in surface albedo occur on the scales seen in the Voyager images and probably on smaller scales too, due initially to internal geological processes and the effects of meteorite bombardment.
Regions that are darker will be warmer, and the ice within them should have a greater sublimation rate, than nearby brighter regions. Because sublimating water molecules on the Galilean satellites `jump' tens of kilometers before re-impacting the surface (Purves and Pilcher, 1980), any imbalance in sublimation rates in regions less than tens of kilometers apart will result in a transfer of ice from the dark regions to brighter ones. If addition of ice brightens the bright regions, and loss of ice darkens the dark regions, the transfer of ice will be enhanced by positive feedback, and will only be halted when almost all ice has been lost from the surface of the dark regions. The result will be very efficient segregation of an initially fairly homogeneous surface into a patchwork of bright icy and dark ice-free areas.

Timescale for Segregation

The process of ice segregation is halted when the darker surface regions become covered in a lag deposit of non-ice particles that cut off further sublimation. The segregation timescale t_Sis thus given by the thickness of surface ice x containing enough non-ice particles to cover the surface, divided by the diurnally averaged net rate of surface lowering due to sublimation, S_N:

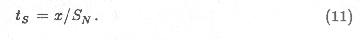
x is the thickness of ice containing, per unit area, unit total cross-sectional area of non-ice particles. If the volume fraction of non-ice particles is f_P, and their radius is r_P, then by simple geometry, assuming spherical particles:

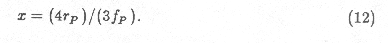
These equations assume a solid surface, without pore space, which is not realistic. However if the surface is porous, with a pore space fraction of p, then x is increased by a factor of 1/p, but surface recession rate S_N is increased by the same factor relative to the solid-ice recession rate. t_S is therefore independent of p.
Sublimation rate can be determined as follows. Assuming instantaneous equilibrium with incident sunlight, and unit emissivity, surface temperature T is obtained from

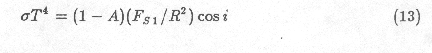
where $\sigma$ is the Stefan-Boltzmann radiation constant, A is the bolometric albedo, F_S1 is the solar constant at 1 A.U., R is the distance from the sun in A.U., and $i$ is the local solar incidence angle, a function of latitude and time of day. The amount of heat removed from the surface due to the latent heat of sublimating ice is too small to affect surface temperatures below about 180^oK (Lebofsky, 1975).
Water vapor pressure over ice as a function of T is obtained from

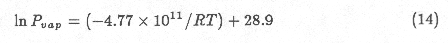
where Pvap is the vapor pressure, and R is the gas constant (all units erg-cgs), which is a fit to experimental data in the range 132^oK--153^oK (Bryson et al, 1974). The instantaneous rate of ice surface lowering due to upward sublimation, s, is then obtained from vapor pressure using

where M is the molecular weight of water, and rho is the density of ice (taken as 0.92 g cm^-3: see remarks above about surface porosity). Water sublimation rate is thus obtained as a function of time of day, and diurnal averaging over i gives the mean sublimation rate S.
S is merely the upward sublimation rate. The net rate S_N will be reduced by the influx of molecules onto the region in question from its surroundings. The influx rate will be the areal mean sublimation rate of ice over a surrounding region tens of kilometers across, weighted by the Maxwell/Boltzmann distribution of molecular jump distances. However, the variation of ice vapor pressure with temperature is so extreme that, for instance, a change in albedo from 0.4 to 0.5 reduces ice sublimation rate by a factor of almost 6 at the equator on the Galilean satellites (from Equations 13, 14, and 15, and Fig. 34 (Chapter 9). If the region being considered is significantly darker and warmer than its surroundings (and it will become darker as segregation progresses) its own sublimation rate will be enough greater than the average influx that S_N will be comparable to S. Use of S instead of S_N should give the segregation timescale to an order of magnitude.
The albedo A of the sublimating surface will decrease as segregation progresses, which will reduce the timescale t_S but further complicate its determination. However, assuming a constant A should allow order-of-magnitude timescales to be determined.
Figure 31 shows the segregation timescale t_S as a function of albedo and latitude, at Jupiter's distance from the sun (R = 5.2 A.U.). Non-ice particle size r_P and volume fraction f_P were held constant at 0.1 mm and 0.01 respectively, giving x a value of 13 mm. From Equations 11 and 12, t_Sis proportional to r_P and inversely proportional to f_P, allowing calculation of t_S from Fig. 31 for other values of these parameters.
For dark or moderate albedo ice at low latitudes, t_S is remarkably small, indicating surface segregation on timescales of years or decades. Given the assumptions of the model, which are discussed in more detail below, equatorial regions on the icy Galilean satellites are very unstable with respect to this process. Segregation is dramatically slower at high latitudes because of the extreme temperature dependence of ice sublimation rates.
On the Saturnian satellites (R = 9.5 A.U.), assuming the same particle properties as for Jupiter, t_S has a value of 10⁸ years for 0.4 albedo equatorial ice, and at Uranus (R = 19.2 A.U.) t_S is nearly 10¹⁴years even for 0.0 albedo ice at the equator. Clearly the proposed model for ice behavior is not relevant to the Uranian satellites, and its importance at Saturn is doubtful. I am concerned here only with the Galilean satellites, where thermal segregation, on the basis of the calculated timescales, may be a very important process.
It should be noted that the ice redistribution I discuss here, which is in response to temperature variations, is quite different from the ice grain growth mechanism proposed by Clark et al (1983). Their model assumes an isothermal surface, the ice redistribution to larger grains being powered by the increase in surface binding energy with the radius of curvature of the grain surface. Grain growth by this process is very slow: their Fig. 3 shows that at 150 ^oK a 0.1 mm grain takes about 50 million years to double in size. However the same grain has a one-way sublimation rate of 0.25 mm yr^-1 (from Equations 14 and 15 above). Temperature gradients within a regolith are inevitable, and if, for instance, the grain's neighbors are at 149 ^oK, with a sublimation rate of 0.19 mm yr^-1, the grain will sublimate at a rate of 0.06 mm yr^-1 and disappear entirely in a year! Smaller temperature contrasts will give sublimation (or growth) rates that are smaller, but contrasts small enough to allow isothermal grain growth to be important seem very unlikely on the Galilean satellites. The redistribution of ice due to temperature gradients within the regolith may, in contrast, be a major influence on regolith structure, though it is not considered further in this dissertation. Smoluchowski and McWilliam (1984) have considered the problem but only in terms of pore migration in solid ice.

Scale of Segregation

The model assumes that the segregating regions are larger than a few tens of centimeters, so that lateral conduction of heat between the regions during a day is unimportant (Chapter 7), and smaller than tens of kilometers, so that each can receive a full flux of sublimated water molecules from the other. Within these very generous limits of scale, the physics of the problem is the same. However, the fact that the Voyager images do not show drastic segregation down to the limit of resolution (typically a kilometer or two) means that any segregation is at scales smaller than this. There is an exception at high latitudes on Callisto, where topographically associated segregation, probably thermally controlled, is visible in the Voyager 1 images on a scale of tens of kilometers (Spencer and Maloney, 1984, and Fig. 32). This example is discussed shortly.

Assumptions

The assumptions implicit in the above discussion of the segregation mechanism, and the derivation of timescales, are now listed and discussed explicitly.
1) Dirty ice surfaces darken as they lose ice by sublimation. The dark particles released by the sublimating ice would be expected to accumulate on the surface and thereby darken it, eventually forming an ice-free lag deposit. However, it is possible that formation of a lag deposit is prevented because the dark particles, rather than remaining on the surface, sink beneath it. Dark particles on the surface may warm the ice immediately around them, causing local sublimation around the particle and eventually creating a hole that it can sink into. Darkening of the surface and attendant positive feedback might thus be prevented. There is evidence from Viking observations that a phenomenon of this type occurs on the Martian CO₂ polar caps (Paige, 1985). Such particle sinking has not been observed for dirty water ice mixtures in the laboratory, despite attempts to provoke it (by Purves and Pilcher; Clark, pers. comm.) but cannot be ruled out as a possibility.
Another way of violating assumption 1) may be if dark particles embedded in the ice brighten as they lose their ice coating, due to an enhanced refractive index contrast at their surfaces. Sublimation from a dark dirty ice surface could thus brighten it somewhat. However the surface can only be brightened to a maximum albedo equal to that of the dry grains themselves. As most common non-ice materials in the solar system have lower albedos than most icy surfaces, it is unlikely that this brightening effect is sufficient to prevent segregation.
2) Dirty ice surfaces get brighter as ice is deposited on them. This is generally the case experimentally (see e.g. Fig. 16 of Clark, (1981)), but laboratory deposition rates are much faster than the mm yr^-1 rates relevant to the Galilean satellites. It is possible that ice depositing on an already-icy surface at low rates forms a surface `glaze' that lowers, rather than raises, the albedo. G.T. Sill (pers. comm.) notes that when he has deposited water ice from vapor onto a smooth surface at about 130 ^oK, it is initially smooth and glassy but becomes bright after it has reached a few microns thickness. The lower the deposition rate the darker the ice at a given thickness, and actual deposition rates will be a couple of orders of magnitude slower than Sill has observed in the laboratory. The effect on albedo of very slow ice deposition onto an already rough surface has not been investigated, though nucleation of discrete grains seems more likely than on a smooth surface. Bombardment by heavy ions is known to rapidly brighten glassy ice surfaces (Brown et al, 1978) but results in `welding' of fine-grained frost (Clark and Nelson, pers. comm.) and thus is also an important factor. More experimental work is clearly needed in this area. The segregation model I describe here requires the albedo to increase as ice is deposited, and will not work if a dark glaze forms on the brighter regions and makes them as dark as the rest of the surface.
There is evidence from the appearance of the surface of Callisto in particular that supports assumptions 1) and 2). The evidence comes from Callistoan high latitudes (Figure 32), where bright deposits are visible on the north-facing slopes of craters, and south-facing slopes are darker than their surroundings (Spencer and Maloney, 1984). If one accepts the simplest explanation of the topographically controlled albedo patterns, they imply formation of a dark lag deposit (or something equivalent) on the warmer south-facing slopes, and brightening of north-facing slopes due to ice deposition. The explanation may be more complicated than this, as a small region near Gilpul Catena shows bright east-facing, rather than north-facing, slopes, but the northward orientation is much more widespread, supporting a thermal origin for the albedo patterns.
\figinsert \vbox{\vskip 5 truein} Fig. 32. Image of Probable Thermally Segregated Ice on Callisto. A high latitude Voyager 1 image (FDS 16424.48). Bright patches of ice are visible on cooler north-facing slopes, resulting in an apparent reversal in illumination direction (arrow shows the true direction of solar illumination). Latitude/longitude grid from Davis and Katayama (1981). From Spencer and Maloney (1984).
3) Daytime surface temperatures of darker ice are not dramatically less than predicted on the basis of equilibrium with sunlight. Daytime temperatures of a homogeneous surface will be 5 ^oK to 10^oK less than equilibrium temperatures (Chapter 7). Segregation timescales for a homogeneous surface may thus be a factor of several longer than shown in Fig. 31, but will be of comparable magnitude. Bright ice, contributing little to the daytime thermal flux, may have high thermal inertia but only exists if segregation has already occurred. Assuming unit emissivity for the moment, the actual surface kinetic temperature of the ice might be different from the infrared effective temperature because thermal emission comes not from the surface but from a finite depth. However the discrepancy is probably small because of the high opacity of ice to thermal infrared radiation.
At 40 microns, near the peak in the blackbody curve for daytime ice temperatures, the absorption coefficient for water ice is 0.104mic^-1 (Fig. 5, Chapter 4), so unit optical depth occurs in a thickness of about 9 microns, and thermal emission will originate preferentially from around this depth into the surface. The kinetic temperature at 18 microns depth must therefore be comparable to the observed effective temperature of the thermal radiation. Even given the low thermal conductivities of the surfaces of the Galilean satellites (Chapter 7) there must be less than a degree or so temperature drop between 9 microns depth and the actual surface, or the conducted heat flux toward the surface would exceed the total radiated heat flux. Therefore the kinetic temperature of the very surface of the ice, which determines sublimation rates, is probably very close to the observed effective temperature of the surface. This conclusion is independent of the details of where in the regolith the sunlight is absorbed.
Another related way that surface ice might be colder than the effective temperature of the thermal radiation would be if the radiation came mostly from the embedded dark particles rather than the ice itself. However, because of the ice opacity, only particles within tens of micron of the surface can radiate to space. The great transparency of ice in the visible means that most of the incoming solar radiation will be absorbed much more deeply than this, by particles that can only lose their absorbed heat by conduction to the surrounding ice. The ice itself must eventually lose this heat by radiation and must thus emit the bulk of the radiated flux. The ice must therefore be as warm as the effective temperature of the radiation.
Non-unit emissivity would increase kinetic temperature compared to infrared effective temperature, though low values are unlikely due to the abovementioned high thermal infrared opacity of ice, and the particulate nature of the surfaces.
Apart from these probably small effects due to the non-zero infrared transparency of the ice, the temperature of thermal emission should provide a good guide to the expected sublimation rate. Shoemaker et al (1982) suggested that surface roughness could dramatically reduce sublimation rates (sublimating molecules could be blocked by surface projections), but this seems unlikely, as the projections will be sublimating themselves. Regardless of the roughness of the surface, if an infrared photon can escape to space from a surface region at a particular temperature, a sublimating water molecule should be able to do the same.
4) Dark regions are warmer at the surface during the day than bright regions. This will be true unless dark regions have significantly higher thermal inertia or emissivity than bright regions. However, as discussed above, the thermal inertia of the dark regions cannot be very high (because of the overall low thermal inertia), and the emissivity of icy regions is probably close to unity. It is concievable that small albedo variations are prevented from growing because correlated small variations in thermal inertia or emissivity prevent the expected temperature contrasts, but there is no obvious reason to expect such a correlation. Voyager IRIS observations of Ganymede show the expected correlation between regional albedo and daytime effective temperature (Chapter 5), which provides some confidence that the same may be true on local scales.
5) Other processes do not redistribute the ice more rapidly than thermal sublimation. This possibility is considered at some length in the next chapter. The conclusion is that thermal sublimation is so rapid that neither micrometeorite bombardment nor ion sputtering can compete with it at low latitudes on Ganymede, Callisto, and perhaps Europa. At high latitudes and on Europa sputtering or perhaps micrometeorites might prevent segregation.
Assumptions 1 thru 5 thus appear to be at least probably valid, though not proved. If the assumptions are correct, segregation by thermal sublimation, at rapid rates comparable to those shown in Fig. 31, is a very probable process on the icy Galilean satellites, especially at low latitudes on Ganymede and Callisto. Indirect observational evidence that segregation has indeed occurred on Ganymede and Callisto is discussed in Chapter 11.

CHAPTER 9 COMPETING ICE TRANSPORT PROCESSES

Other surface transport processes may compete with the thermally-controlled ice segregation discussed in the last chapter, tending to re-mix the segregated materials. Leaving aside internally-driven geological activity, which at least on Ganymede and Callisto is not currently important, the important competing processes, micrometeorite bombardment and ion sputtering, are considered in this chapter.

Micrometeorite Bombardment

The micrometeorite environment of the Galilean satellites is still poorly known. Pioneer 10 detected a flux of particles in the region of Ganymede and Callisto that was enhanced over the fairly constant values recorded since leaving Earth by a factor of about 100 (Humes et al 1974). Recently, Zook et al (1985) have successfully modeled the Pioneer detections on the assumption that the particles originate on the inner small Jovian moons and then move outwards, in prograde orbits, under the influence of plasma drag. These are particles capable of penetrating the 25\mic-thick steel of the Pioneer detector and are thus responsible for regolith gardening to depths of tens of microns (or maybe somewhat shallower, as impact velocities on the satellites will be smaller than on Pioneer).
Figure 33 compares rates of regolith gardening on the Earth's moon as a function of depth, according to numerical models and observational constraints from Apollo, with expected diurnally-averaged ice sublimation rates on the Galilean satellites for various ice albedos. Also shown is the expected 100-fold enhancement of gardening rates on the Galilean satellites compared to the moon, at least in the depth range of a few tens of\mic, suggested by the Pioneer results. In this depth range it appears the surface may be turned over in 50 years or so: an equivalent rate of a few X 10^-3 mm yr^-1. For greater depths it is likely that the population of gardening micrometeorites is dominated by gravitationally-focused interplanetary dust, which will be enhanced over interplanetary values by a factor of ten or less (Humes, 1980) for reasonable size-frequency distributions, giving consequently lower gardening rates. If the model of Zook et al (1985) is correct, and the particles are in near-circular prograde orbits, impact fluxes should be similar on both leading and trailing satellite hemispheres. It should be noted, however, that an alternative model in which the Pioneer dust is derived from outside the Jovian system, and impacts Europa and Ganymede primarily on the trailing hemisphere (but Callisto mostly on the leading hemisphere) has been developed by Hill and Mendis (e.g. 1981), and also claims to explain the Pioneer data.
Fig. 33 shows that, even including the likely enhancement of gardening rates near Jupiter when compared to the moon, equatorial water ice with a bolometric albedo of less than about 0.5 will sublimate at a rate faster than the rate of impact gardening. Ice with an albedo of 0.2 that is surrounded by brighter material, and is thus sublimating water at a rate comparable to the one-way rate shown in Fig. 34, will lose 0.1 mm of ice to its surroundings in a few months, while micrometeorite gardening would take decades to redistribute this thickness of material. Segregation is controlled by sublimation of the ice in the warmer, darker, surface regions, so unless most of the satellite surface has a bolometric albedo higher than about 0.5, as is probably the case on Europa (Chapter 7), impact gardening will not affect segregation in equatorial latitudes.
At higher latitudes, of course, sublimation drops precipitously. Figure 34 shows one-way sublimation rates as a function of ice albedo and latitude, as well as the estimated rate of impact gardening derived from Fig 33. Gardening rates exceed sublimation for dark ice poleward of about 60^olatitude.
Even a vertical impact gardening rate in excess of sublimation may be unable to prevent segregation, however. This is because sublimation, with mean molecular jump distances of tens of km., is much more effective at lateral transport than impact processes, where most of the material lands within a crater radius of the crater rim. Impacts can only re-homogenize the surface laterally over length scales comparable to the size of the largest ejecta blankets that cover most of the surface in the time interval being considered. This distance will be, to an order of magnitude, ten times the depth of regolith mixing (because ejecta blanket diameter is typically twice crater diameter, and the diameter is typically about five times the crater depth for small craters (e.g. St\"offler et al 1975)).
If 10³ years of impact gardening mix the top 1 mm of the surface, lateral mixing will only have occurred up to centimeter length scales. Even if a darker region of the surface is sublimating ice at a net rate much smaller than the rate of vertical mixing by impacts, significant ice depletion of that region can still occur in 10³ years provided the region is larger than a few cm., and complete segregation can eventually follow. The main effect of the impact gardening will be to slow down the rate of ice depletion and lag deposit formation in the darker regions, by increasing the thickness of surface material from which ice must be removed. Another effect may be to increase the minimum allowable size for the segregated patches.
There will probably be some sublimation rate below which impact gardening will prevent segregation from occurring at all. Using the arguments of the previous paragraph this minimum rate will be much lower than the gardening rate, but detailed quantification of the effect of impact mixing in these circumstances will require sophisticated computer modelling.
I conclude that impact gardening by micrometeorites is unlikely to affect thermal ice segregation except possibly on the very bright surface of Europa and at high latitudes on Ganymede and Callisto. Even in these places the reasoning outlined above suggests that impacts will probably merely slow the segregation process rather than preventing it. However in areas where sublimation rates are much lower than gardening rates segregation may be prevented.

Ion Sputtering

Unless the icy satellites have substantial magnetospheres or atmospheres (Wolff and Mendis, 1983) their surfaces will be bombarded by the abundant ions in Jupiter's magnetosphere, resulting in sputtering of surface ice (e.g. Brown et al, 1978), which will act to counter the thermal segregation process. Unlike micrometeorite bombardment, sputtering is a very efficient means of lateral transport of ice. Molecules typically leave the surface with an appreciable fraction of escape velocity and travel hundreds of kilometers before re-impacting (Seiveka and Johnson, 1982). There is also some net erosion of the surface, as a fraction of the sputtered H₂O molecules are dissociated by the incoming ion (Brown et al 1982). If sputtering rates are greater than thermal ice sublimation rates segregation will thus be prevented, as ice distribution will be re-homogenized on all scales up to and greater than the largest scales at which thermal segregation can occur.
Appendix D discusses the likely rates and geometry of sputtering on the three icy satellites, and the rates, from Tables VIII and IX, are compared to sublimation rates in Fig. 34. Sputtering is most intense on Europa, and if the high energy plasma is dominated by heavy ions erosion rates on the trailing hemisphere may approach sublimation rates for ice with Europa's bolometric albedo of around 0.62 (Buratti and Veverka, 1983). Moderate enhancement of sputtering over estimated rates, or reduction in sublimation due for instance to small but finite thermal inertia (Chapter 7), might be sufficient to prevent segregation here. Sputtering rates on Europa's leading hemisphere are probably less but are hard to calculate. On Ganymede and Callisto, because of the lower ion fluxes and lower albedos, it is very unlikely that sputtering can prevent segregation except at high latitudes.

CHAPTER 10 SPECTROSCOPIC EVIDENCE FOR ICE DISTRIBUTION AND ABUNDANCE

The previous two chapters have indicated the likelihood of the segregation of dirty ice surfaces at Jupiter into regions of pure, bright, ice and regions covered by a dark, ice-free lag deposit. The reflectance spectra of the satellites contain information on the actual distribution of ice on their surfaces, and in this chapter I consider this evidence and ask whether it is consistent with the segregation of ice on the Galilean satellites.

Absolute Reflectance Levels

Figure 35 shows the satellite spectra, taken from Clark (1980) and Lebofsky and Feierberg (1985). The Clark spectra are given in relative form, and I now discuss in some detail the derivation of the absolute geometric albedos, which are critical to some of the following analysis.
Johnson et al (1983), Fig. 1, shows absolute geometric albedos for the Galilean satellites at specific orbital phases and at zero solar phase angle (neglecting the opposition effect), as a function of wavelength. This plot is obtained from a combination of the earth-based spectral data of McFadden et al (1980), the absolute V filter geometric albedos, adjusted for orbital phase, from Morrison and Morrison (1977), and the Voyager satellite diameters. The albedos are consistent with separately calibrated Voyager disk-integrated photometry shown on the same plot.
From this plot it is possible to adjust the 0.8\dmic\ geometric albedos to the orbital phases of the Clark (1980) spectroscopic observations, again using the V filter (0.55\dmic) orbital phase curves of Morrison and Morrison (1977) and the assumption that the 0.8/0.55\dmic\ brightness ratio is independent of orbital phase. This assumption is justified for Ganymede and Callisto by the constancy of the 0.73/0.56\dmic\ brightness ratio all around the orbit as shown in Fig. 12 of McFadden et al (1980). The ratio for Europa is also fairly constant over the range of orbital phase between the Johnson et al (1983) Fig. 1 spectrum at 293^o and the Clark (1980) spectrum at 243^o. The resulting 0.8\dmic\ geometric albedos are used to scale the Galilean satellite spectra shown in Fig. 35 and subsequent figures.

Method of Analysis

Recent interpretations of the spectra by Clark (1980) favor homogeneous, rather than segregated, surfaces, and would rule out the model for ice behavior presented here. Could the spectra also be consistent with segregated surfaces While determination of the spectrum of an intimate mixture of several materials is highly complex, if the materials are optically isolated the problem is simple, given the spectra of the components. The integrated spectrum is simply the mean of the individual spectra, weighted by the fractional areal coverage of each component. The individual spectra must, of course, be in the form of absolute reflectance. Pollack et al (1978) used this method to match the spectrum of Ganymede, with similar results to those obtained here. Clark (1980) also uses the technique for matching Callisto's spectrum with a segregated surface, but rejects the resulting match for reasons that may not be compelling (see Callisto discussion below).
Plausible candidates, with known spectra, are required for the various postulated surface components. Pollack et al (1978) used theoretical spectra for particulate surfaces containing ice and bound water, whereas here I use experimentally determined spectra of frosts and carbonaceous meteorites. The spectra of other satellites are also used, as they certainly represent plausible candidate surface components.
A possible candidate for the dark component on the satellite surfaces is carbonaceous chondritic material, though various hydrous or anhydrous silicate mineral assemblages (such as Fe³⁺-bearing silicates (Clark, 1980)) are also possible. Figure 36 shows the near infrared spectra of two carbonaceous chondrite meteorites, Orgueil (Feierberg, unpublished data) and Murchison (Lebofsky et al, 1982). Both are featureless apart from a deep absorption feature in the 3\dmic\ region, due to structural OH and adsorbed water. The overtone bound water absorptions at 1.9 and 1.4 microns (e.g. Clark, 1981) are not visible in either spectrum, being masked by the dark material in the samples. Although the data from Orgueil do not extend shortward of 1.6 microns, other data for this meteorite in the 0.5--2.5 microns range (Johnson and Fanale, 1973) show a flat spectrum down to 0.7 microns, and this flatness is assumed in combining Orgueil with other spectra below.

Ganymede

Fig. 8 of Clark (1980) shows Ganymede's leading hemisphere spectrum in the 0.7--2.5 microns region to be almost identical to that of a laboratory frost-on-ice spectrum, except that Ganymede has a lower absolute brightness. As Clark states, the reduced brightness could be due to a small amount of dark material mixed in with the frost. However the presence of segregated very dark ice-free material could also reduce the absolute brightness level without otherwise affecting the spectrum. Almost all the light would still come from the frost, but the frost's areal coverage would be reduced. Provided that the non-ice component was much darker than the frost (likely to be true except in the 3\dmic\ region) the areal fraction of frost would be given on this model by the brightness ratio between the Ganymede and frost spectra.
The absolute reflectance of the frost-on-ice at 1 micron is 0.78 (Clark, pers. comm.). The geometric albedo of the leading hemisphere of Ganymede at this wavelength is 0.48, from Fig. 35, but this must be converted to a reflectance for comparison with the frost.
The ratio geometric albedo / reflectance depends on the photometric properties of the surface: it is unity for a planet with a lunar-like surface, i.e. one that shows no limb darkening at zero phase, and 2/3 for a Lambertian scatterer. Squyres and Veverka (1981) show that at around 0.47 microns the surfaces of Ganymede and Callisto are photometrically lunar-like, with little limb darkening, so that reflectance and geometric albedo are about equal. More Lambertian behavior might be expected at 1 microns due to the higher albedo, but even high albedo craters on Ganymede show lunar-like photometry at 0.47 microns, with reflectances (and thus albedos) as high as 0.7. It is therefore likely that the average surface at 1 micron, with a geometric albedo of 0.48, is also lunar-like, so that its reflectance is also close to 0.48. This includes contributions from bright polar caps and ray craters so the reflectance of the `normal' surface may be a little lower.
Squyres and Veverka (1981) give an average geometric albedo for Ganymede at 0.47 microns of 0.43 from Voyager data. Application of the orbital lightcurve of Morrison and Morrison (1977), Fig. 16.3, which shows the trailing hemisphere 0.05 magnitudes darker than the average surface, gives a 0.47\dmic\ albedo of 0.41 for the trailing hemisphere. This is brighter than the value of 0.37 obtained from Voyager and groundbased data of the trailing hemisphere by Johnson et al (1983) Fig. 1. Because the Johnson et al Voyager value is obtained in a more direct manner (from low phase angle full-disk images rather than extrapolation from high phase angle images) and agrees with the groundbased values it is used here in preference to the Squyres and Veverka albedo.
So using 1\dmic\ reflectances of 0.48 for the Ganymede leading hemisphere and 0.78 for the frost-on-ice, Ganymede is 0.62 times as bright as the frost. Considering normal reflectances alone (a more accurate analysis would require comparison of laboratory and planetary photometric behavior at a wide range of viewing geometries and wavelengths), it follows immediately that the spectrum of Ganymede is consistent with a surface with a 62 % coverage of frost-on-ice and 38 % coverage of black material that contributes nothing to the spectrum. Although no surface material can be entirely black, material such as that of the abovementioned Orgueil is very dark compared to water frost, and Figure 37 successfully matches Ganymede's spectrum with a linear combination of 55 % frost-on-ice (the same spectrum used by Clark) and 45 % Orgueil. Assuming a non-ice density of 2.5, this is equivalent to 33 % ice by weight in the uppermost surface.
The Orgueil component contributes so little light that the spectrum is still essentially the same as the frost spectrum, except for the reduction in absolute brightness caused by the reduced areal coverage of frost. In particular, if the depths of the shallow 1.04 and 1.25\dmic\ features, not easily seen on Fig. 37, are consistent with a homogeneous surface of almost pure ice, they are also consistent with a segregated surface with 45 % coverage of dark material. The depths of these minor bands cannot be used to rule out a segregated surface on Ganymede because these depths vary very little with increasing fractional coverage of dark material, until a large fraction of the 1\dmic\ region light comes from the dark component.
Water ice is so dark in the 3\dmic\ fundamental absorption band, especially in the 2.8--2.9\mic\ region where the real refractive index is low, that the light from the dark component is no longer negligible. The minimum geometric albedos of J2 (leading hemisphere), J2 (trailing), J3, and J4 in the 2.9 microns region are 0.001, 0.005, 0.011, and 0.035 respectively (Lebofsky and Feierberg, 1985 and pers. comm.) while that of Orgueil is about 0.015. So although Ganymede is very dark in this region, it is much brighter than Europa and over half as bright as Orgueil, which is ice-free. Ganymede's 2.9\dmic\ albedo is thus compatible with a surface composed of 45 % Orgueil-like material and 55 % icy material with a 2.9\dmic\ albedo of 0.0043, much brighter than the leading hemisphere of Europa in this region and therefore not unreasonably dark for icy material at Jupiter.
It appears, therefore, that from 0.7 micron to the 3\dmic\ region, Ganymede's leading hemisphere spectrum can be interpreted as due to a surface with 55 % pure water ice and 45 % carbonaceous chondritic material. The redness of the spectrum in the visible region, however, requires the addition of a minor contaminant in the water ice, as noted by Clark (1980). It is possible that a contaminant cannot redden the frost sufficiently in the visible without reducing the brightness at all wavelengths to the point where the frost is as dark in the near-infrared as Ganymede itself. In this case the segregated surface interpretation of the spectrum suggested here is no longer possible. Unfortunately the laboratory spectra of dirty ices in Clark (1981) do not extend into the visible so direct data is not available. Fig. 13 of that paper, however, shows that addition of 5 % areal coverage `red cinder' sprinkled on frost greatly reduces the frost reflectance shortward of 1 micron but has little effect at longer wavelengths. It seems likely from this figure that a smaller coverage of cinder would redden the frost only in the visible region with little effect in the infrared, in which case the redness of Ganymede does not preclude a segregated surface. More experimental work would be needed to verify this.
The match to Ganymede's leading hemisphere spectrum suggested here is similar to that of Pollack et al (1978), who, using theoretical spectra, inferred a surface with about 65 % ice coverage and 35 % of a dark non-ice containing bound water to reduce the 3\dmic\ albedo to the observed value. They assumed a brighter non-ice component than used here, which may account for the difference in areal ice coverage.
I should stress that the above discussion of Ganymede's spectrum merely demonstrates the feasibility of a segregated surface. It shows that our current knowledge of the spectrum does not rule out the kind of segregation implied by the model presented in Chapter 8. A homogeneous, dirty-ice model may be equally consistent with the spectrum.

Callisto

Callisto's leading hemisphere spectrum in the 0.7--2.5 microns region can also be matched quite well with a linear combination of the frost-on-ice and Orgueil spectra. Figure 38 shows the best-fitting linear combination of the above candidate spectra to have been found by `eyeball' techniques, comprising 9 % frost-on-ice and 157 % Orgueil, or 91 % material like Orgueil but having 1.73 times its absolute reflectance at all wavelengths. The greater reflectance could be brought about by a decreased grainsize, or decreased organic content compared to the Orgueil sample measured by Feierberg. Such changes would doubtless alter the depth of the bound water absorption at 3 microns, but comparison of the Orgueil and Murchison spectra in Fig. 36 shows that this depth is very variable between different meteorites in any case. This fit corresponds to only 4 % ice by weight for a non-ice density of 2.5.
The fit reproduces the depth of Callisto's 1.55\dmic\ absorption feature very well, though the 2.02\dmic\ feature is somewhat too deep in the model. A better fit to this band, also shown on Fig. 38, is given by a combination of 10 % Europa trailing hemisphere and 180 % Orgueil (90 % material with twice Orgueil's reflectance). The absolute depth of the 2.02\dmic\ band on Europa is reduced due to saturation and this fit indicates that the same may be true on Callisto.
The fit using 10 % coverage of Europa-like ice also matches the depth of the 3\dmic\ feature on Callisto. Now, the depths of the 1.55, 2.02, and 3\dmic\ features are all matched with reasonable accuracy, indicating that the gross features of Callisto's leading hemisphere spectrum up to 3 microns are consistent with a checkerboard surface including only 10 % coverage of water ice. There is, however, a large discrepancy beyond 3.3 microns that I discuss later.
Clark (1980) shows a very similar fit to Callisto's leading hemisphere spectrum, but rejects it using two arguments:
1) The fit is inconsistent because it gives different ice surface coverage depending on the wavelength considered. The numbers given to support this argument seem to be derived using the incorrect assumption that one-third of the light comes from the ice component at all wavelengths (at least, use of this assumption results in the numbers for derived surface coverage that are given in the paper). When this error is corrected the surface coverage derived at different wavelengths becomes fairly consistent, at least for the 1.55 and 2.02\dmic\ bands.
2) The 1.25\dmic\ band in the model is only half the depth of that on Callisto. However, a very similar discrepancy for the 1.25\dmic\ band in the frost-on-ice fit to Ganymede's spectrum in the same paper is not discussed and presumably not considered significant. As discussed below, I do not find the depths of either the 1.25 or 1.04\dmic\ bands to be good evidence against segregation on Callisto. Clark (pers. comm.) has recently pointed out that in any case the measured depth of the 1.25\dmic\ band is unreliable due to instrumental problems.
In contrast to the Ganymede case, the depths of all ice absorption features are substantially diluted if the ice occupies only 9 % or
10 % of the surface, because a large fraction of the integrated light comes from the spectrally neutral dark component (the postulated Orgueil-like material is spectrally neutral in the 1--2.5 microns range). It is therefore necessary to check whether the areal mix postulated above results in reasonable depths for the minor 1.04 and 1.25\dmic\ bands, as well as the major 1.55 and 2.02\dmic\ bands visible in Fig. 38, in the assumed ice component, given the known depths of these features in the integrated spectrum.
Figures 39 and 40 show the depths of the 1.04, 1.25, 1.55, and 2.02\dmic\ bands for a variety of icy laboratory and solar system spectra. The depths of the 1.55 and 2.02\dmic\ features tend to be comparable, and the 1.25\dmic\ feature is generally about twice the depth of the 1.04\dmic\ feature. However the ratio of the depths of the 1.04, 1.25\dmic\ pair and the 1.55, 2.02\dmic\ pair is very variable, and depends on the grain size distribution (not just the mean grain size) of the sample. Figs. 39 and 40 also show the depths of the four bands for the postulated segregated ice component on the leading hemisphere of Callisto, assuming a neutral component of 12% reflectance (the same as the Orgueil-like component in the Orgueil plus frost-on-ice fit of Fig. 38) and areal coverages of this component of 90%, 80%, and 70%. Derivation of these band depths is given in Appendix E. The ice band depths for 20% ice coverage all match rather closely the depths for the trailing hemisphere of Ganymede. The 1.04\dmic\ ice component continuum reflectance for this case (also derived in Appendix E) is 0.47, comparing favorably with the 0.45 geometric albedo at 1 micron of the Ganymede trailing hemisphere (Sill and Clark, 1982). This means that a surface of 20% Ganymede trailing hemisphere, and 80% 0.12 reflectance Orgueil-like material, would match the depths of all four Callisto ice absorption bands, as well as the approximate geometric albedo at 1\mic. If the Ganymede trailing hemisphere, like the leading hemisphere discussed in the Ganymede section above, could be matched with approximately 50% ice coverage, this would again indicate about 10 % ice coverage on the leading hemisphere of Callisto. Unfortunately I do not have a complete Ganymede trailing hemisphere spectrum available to test this match.
The closeness of the match between the band depths of the Callisto leading hemisphere ice component and the trailing side of Ganymede is probably fortuitous, but serves to show that the observed band depths on Callisto do not rule out an ice-poor, segregated interpretation of the spectrum. Even the ice component spectrum for an assumed 10% ice coverage shows band depths well within the envelope of laboratory frost and frost-on-ice spectra, and might represent a plausible interpretation. The 1.04\dmic\ continuum reflectance for the ice in this case is 0.82, which is reasonable for almost pure ice (see e.g.\ Clark, 1981 Fig. 6).

Table VI. 2-Component Fits to the Spectrum of Callisto

`Y' indicates that the fit matches the data, `N' indicates an inconsistency, and `--' indicates that the fit does not give information on this feature of the spectrum. See text for more detail.


Icy Comp- onent	Icy Frac- tion	Non-ice Component	1-um Albedo	Continuun Shape	1.04	Band 1.25	Depths 1.55	2.02	3.0	Shape >3 um
Frost-on- Ice	9%	Orgueil X 1.73	Y	Y	-	-	Y	N	-	-
Europa Trailing	10%	Orgueil X2.00	Y	Y	-	-	Y	Y	Y	N
Ganymede Leading	20%	Neutral (A=0.12)	Y	-	Y	Y	Y	Y	-	-
Plausibel Ice	10%	Neutral (A=0.12)	Y	-	Y	Y	Y	Y	-	-

Table~VI summarizes the Callisto discussion with a truth table for the four possible spectrum matches mentioned above. `Plausible Ice' refers to the 10% ice component in the previous paragraph. The `neutral (A=0.12)' component in the last two fits need be neutral only in the 1.0--2.5 microns region considered in these fits, with a 12% albedo. It is thus similar to the brightened Orgueil component of the first two fits. The four fits are largely consistent with each other, especially if the Ganymede trailing hemisphere in the third fit, like the Ganymede leading hemisphere discussed above, is consistent with a 50/50 ice/non-ice mixture, so that 20% Ganymede trailing hemisphere is equivalent to about 10% ice.
These results for Callisto are similar to those of Pollack et al (1978) in that the bulk of the surface is found to be covered in ice-free material containing bound water. They also mentioned that the spectrum suggested the presence of a `very minor amount of water ice' but did not estimate its abundance. Recently, Clark et al (1986) have recognized that the brightness of Callisto at 3 microns requires the presence of `some patches' of ice free material but have not estimated the abundance of such material.
The matches suggested here have a brighter non-ice component on Callisto than on Ganymede. Attempts to match Ganymede's spectrum using the frost-on-ice spectrum and the same brightened Orgueil component used in the Callisto match are rather too bright in the 3\dmic\ region, and have too deep a 2.02\dmic\ band. My modelling is not exhaustive enough to conclusively prove a non-ice albedo difference between the objects, however. It is possible that by using different candidate spectra for the two components a match can be made that allows the same non-ice component on both bodies.

Europa

Europa's spectrum is unusual, as Clark (1980) notes. The great breadth of the 1.55 and 2.02\dmic\ features indicate a large effective grain size for the surface ice, though coarse-grained ice does not provide a good match to the overall spectrum shape. The leading hemisphere of Europa is so dark in the 3\dmic\ region (minimum A = 0.001, darker than `normal' pure water ice) that any segregated non-ice component present in significant quantities must be much darker than even Orgueil in this region (A = 0.035), and I am unaware of any suitable material. The leading side of Europa probably therefore has very little segregated non-ice on its surface.
The trailing hemisphere is bright enough in the 3\dmic\ region (0.005) to allow, for instance, 11% areal coverage of Orgueil-like material if the remaining ice is as dark as the leading side, but the overall strangeness of the spectrum makes detailed interpretation risky. Also, the trailing hemisphere receives most of the ion flux and is the most likely place for sputtering to prevent segregation. Therefore, the fact that it is brighter than the leading hemisphere at 3 microns probably isn't due to more thermal segregation on the trailing side, but is an indication of some other process.

Interpretation of the Spectra Beyond 3 microns

The model fit to Callisto in Fig. 38 breaks down beyond 3.1 microns, where Callisto is much darker than the model. In fact, as noted by Lebofsky and Feierberg (1985), all the icy Galilean satellites are anomalously dark between 3.3 and 3.9 microns, compared to the satellites and rings of Saturn, and laboratory spectra of water ice, which show a strong peak at around 3.5 microns. A large ice grain size might explain Europa's uniform darkness longward of 3\mic, but can't explain the steady increase in albedo with wavelength with no 3.5\dmic\ peak at all, as is seen on Ganymede and Callisto.
Though there may be other explanations of the spectrum shape in this region, an intriguing possibility is the presence of sulfuric acid on the satellite surfaces. Figure 41 shows that the acid is considerably more absorbing in the 3.5\dmic\ region than is water ice, and a small quantity on the surface could produce the required darkening in this region. Sill, (1976, Fig. 25) shows > 50% transmission at all wavelengths short of 2.7 microns through 50 microns of liquid sulfuric acid, so a surface layer 10 microns thick, for instance, could drastically reduce 3.5\dmic\ reflectance and have very little effect shortward of 2.7 microns.
The signature of probable implanted magnetospheric sulfur has been observed in the UV spectrum of Europa (Lane et al, 1981), though not the other icy satellites. Impact processing of implanted sulfur in water ice would probably generate at least some sulfuric acid. A small amount of indigenous sulfur is also a possibility. There is, however, no spectroscopic evidence for other sulfur compounds that might be expected as a result of the reaction of the acid with the non-ice components on the satellite surfaces.

Summary of Spectral Evidence

The spectra of Ganymede and Callisto in the near infrared, including the depths of the minor water ice absorption features, can be modeled to reasonable accuracy by a combination of optically isolated frost-on-ice and carbonaceous chondritic material, with the frost component occupying 55% of the surface of Ganymede, and 10% of the surface of Callisto. Europa is so dark at 3 miccrons (at least on the leading hemisphere) that a significant segregated non-ice component is unlikely. The darkness of the satellites at 3.5 microns might be explained by the presence of magnetospherically- or internally-generated sulfuric acid on the surface.
I claim no uniqueness for the above spectral interpretations. My aim is more to show that the spectral evidence currently available does not rule out the type of segregated surface predicted by the model of ice migration presented in Chapter 8, at least for Ganymede and Callisto.

CHAPTER 11 INDIRECT EVIDENCE FOR SEGREGATION, AND IMPLICATIONS

This chapter sums up the discussion of possible ice segregation on the icy Galilean satellites with some indirect lines of evidence for segregation, and a summary of the implications of this surface picture.

Indirect Evidence

Preservation of Albedo Contrasts

Large albedo contrasts occur at low latitudes on both Ganymede and Callisto. Bright ray craters occur in close proximity to much darker terrain on both objects, and on Ganymede bright grooved terrain occurs next to darker cratered terrain with no gradation in albedo between them at the kilometer resolution of the Voyager images. If the surface is mostly homogeneous, with the albedo contrasts being the result of slightly different concentrations of a minor dark contaminant in the ice, or a grain-size contrast, the ice in the darker regions must be significantly warmer, and have a higher sublimation rate, than in the neighboring bright areas.
For instance, the diurnally averaged sublimation rate of low thermal inertia ice in a bright equatorial ray crater on Ganymede, with a bolometric albedo of 0.5, for instance, is 0.014 mm yr^-1. (Equations 13, 14, and 15, and Fig. 34). The equivalent rate for 0.25 albedo cratered terrain is 0.62 mm yr^-1. If these regions are within a few tens of kilometers of each other there must be a rapid transfer of ice to the bright region, at a rate much faster than can be counteracted by impact gardening or sputtering, as discussed in Chapter 9.
Given that thermal sublimation is the dominant ice transport mechanism, stability is only possible if ice regions close enough together to `communicate' by sublimation have diurnally-averaged sublimation rates that are very similar. The only obvious ways of achieving such a balance are discussed below:
1) Dark ice has a high enough thermal inertia to reduce its maximum daytime temperature to a value similar to that for bright ice. But on Ganymede we can observe the temperature variations associated with the visible albedo patterns, using the IRIS data (Chapter 5, Fig. 15). The bright ejecta of the ray crater Osiris is some 15^oK colder than its darker surroundings in the mid-afternoon, and dark cratered terrain is warmer than brighter grooved terrain. So this is not a viable way of preventing water migration to the bright regions.
2) Even if dark areas have high brightness temperatures, their actual ice surface temperatures are much lower, so sublimation rates are comparable to the bright regions. This is unlikely for the reasons given in the discussion of point 3 in the `Assumptions' section of Chapter 8.
3) All the ice has a similar albedo, regardless of the large-scale (Voyager image resolution) albedo of the surface. In this case, the ice is segregated and is everywhere at least as bright as the large-scale albedo of the bright ray craters, and the observed albedo variations on Ganymede and Callisto result from varying fractional coverage of ice, on a scale too small to be seen in the images. The existence of a plausible mechanism for producing such segregation, as described in Chapter 8, helps make this alternative the most attractive.
The above arguments for segregation based on the evident stability of albedo contrasts on Ganymede and Callisto cannot be applied to Europa, where local albedo variations are much more subdued. The Voyager images show a generally bright surface punctuated by dark (mostly linear) markings. Such a surface could be stable against transfer of ice from the dark to the bright areas if the bright areas are fairly pure ice and the dark markings contain segregated dark regions and ice at the same albedo as the bright areas. A disk-integrated reflectance spectrum, dominated by the light from the bright areas, would show an unsegregated surface, as is observed.
The problem with Europa is then to explain why its surface has not been subject to segregation. Europa is darker than several Saturnian satellites at visible wavelengths, and is much redder than water ice, and if this is a result of significant amounts of dark impurities in its surface ice the model of Chapter 8 might be expected to operate.
There is a possibility, as discussed in Chapter 9, that sputtering will dominate thermal sublimation on Europa's trailing side and thus prevent segregation, though it is less clear whether the same is possible on the leading hemisphere. Micrometeorite gardening is also possibly sufficient to keep the ice mixed. Alternatively, assumptions 1) or 2) (Chapter 8) may be violated on Europa (e.g. dark particles might sink in warmer surface regions, or ice deposition might glaze and thus darken the surface). There is no a priori reason to expect such different behavior for dirty ice on Europa, except to note that its surface is anomalous in many respects, especially in its reflectance spectrum and photometric behavior (Buratti and Veverka, 1983). It is even possible that active resurfacing preempts segregation (Cook et al (1983).

Lack of Thick Polar Caps

A similar piece of indirect evidence for segregated ice on Ganymede and Callisto is the apparent lack of massive poleward migration of ice on either body. Ganymede's polar caps are extremely thin, as geological albedo boundaries can be seen through them, and Callisto has none at all. Purves and Pilcher (1980), assuming segregated ice with an albedo of 0.6, inferred migration of tens of meters of ice from low to mid-latitudes on both Ganymede and Callisto over the age of the solar system. Unsegregated, warm, ice would suffer much more drastic migration, amounting to redistribution of kilometer thicknesses on Callisto (Spencer and Maloney, 1984). The Chapter 8 segregation model provides a way of avoiding this problem by allowing the ice even on Callisto to be very bright. A high thermal inertia for the ice (as may be consistent with the thermal infrared data: see Chapter 7) could reduce migration rates still further by reducing daytime temperatures. High thermal inertia ice is not possible if the surfaces are homogeneous, because of the observed low thermal inertia of the surface as a whole.

Thermal Infrared Evidence

The thermal evidence for segregation comes mostly from the slopes of the Ganymede IRIS spectra, which imply surface temperature contrasts that are probably not due to topography. See Chapters 4 and 7 for a full discussion. Similar surface coverage of bright and dark materials is suggested by the inferred temperature contrasts on Ganymede. The thermal data is also consistent with a small amount of segregated bright material on Callisto. The limited Europa data suggests a relatively smooth, homogeneous surface with little thermal contrast.

Implications

I have already considered the implications of segregated surfaces for ice mobility (reduced drastically) and spectroscopically-inferred ice abundance (also reduced considerably) on the Galilean satellites. Here I consider some other implications of this picture of the surfaces.

Atmospheres

Cold surface ice implies a lower atmospheric column density of water vapor. Yung and McElroy (1977), assuming an ice albedo of 0.32 for Ganymede (i.e. a homogeneous surface), obtained a surface pressure of O₂, produced by UV photolysis of water vapor, of about 1 $\mu$bar. However, an atmosphere of this density was ruled out by Voyager 1's UVS observation of a stellar occultation by Ganymede, which gave an upper limit for oxygen partial pressure of 10^-5 $\mu$bars (Broadfoot et al, 1981).
Kumar and Hunten (1982) show that variations in water vapor abundance can dramatically affect the development of an O₂atmosphere. A reduction in water vapor abundance of only a factor of ten would put the atmosphere in a `low state' with an oxygen pressure below the Voyager limit. Segregated ice with an albedo of 0.6 would have a subsolar vapor pressure more than 200 times less than ice with 0.32 albedo (Equations 13 and 14), thereby explaining the lack of a $\mu$bar oxygen atmosphere on Ganymede. If, as the current work suggests, Callistoan ice is also segregated, no $\mu$bar atmosphere is expected on Callisto either, although there are no good constraints from Voyager observations.

Subsurface Composition

An unfortunate implication of the segregation model is that surface ice abundances probably don't provide a good quantitative indication of subsurface abundances. Much of the observed non-icy surface component may be in the form thin lag deposits overlying more ice-rich material. Radar observations (Ostro, 1982) should provide a better indication of the subsurface composition. It is therefore comforting that the radar albedos, which probably correlate positively with ice abundance, show the same trend (Europa > Ganymede > Callisto) as the spectroscopically-inferred surface ice abundances (see Chapter 1), which implies, not unreasonably, that more extensive lag deposits form on `dirtier' ice. The dark material may be indigenous or exogenic: in the latter case it has been mixed downwards into the subsurface by impact gardening. The possible presence of lag deposits makes it difficult to use the quantitative surface ice abundance to constrain the origin of the dark material.
Even Callisto's radar signature probably indicates a substantial quantity of subsurface ice, and if the segregated-surface interpretation of Callisto's spectrum is correct and there is only 10% areal coverage of ice on the surface (Chapter 10) the discrepancy may indicate the existence of lag deposits covering an icier substrate. Unfortunately it is not yet possible to determine quantitatively the subsurface ice abundance from the radar returns.

Miscellaneous

High-energy ion sputtering yields for water ice, which are temperature dependant, will be lower on a cold-ice segregated surface, with a factor of four decrease between 150^oK and 120 ^oK in laboratory experiments using 1.5 MeV He⁺ ions (Brown et al, 1982, Fig. 5).
As mentioned in Chapter 4, daytime thermal emission from a segregated Ganymede will be very largely from the dark non-ice. For a 50/50 mixture of ice at 120 ^oK and dark non-ice at 160 ^oK, only 24 % of the thermal emission will be from the ice, though light from the ice may completely dominate the reflectance spectrum. The thermal and reflected spectra will be `decoupled' in that each is dominated by a different surface component.