APPENDIX A
ANISOTROPY OF THERMAL EMISSION
This appendix discusses what is known about the anisotropy, or beaming,
of the thermal emission from individual regions of planetary surfaces.
It also describes the measurement of beaming on the Galilean satellites,
using the IRIS data.
Lunar Observations
Most of the published observations of the directionality of thermal emission
have concerned the Moon (see Saari and Shorthill, 1972, and Saari et
al, 1972 for a summary). It was found that:
1) Emission from a given point peaks in the direction
of zero solar phase, and decreases with increasing phase angle.
2) The zero-phase enhancement is greater at larger
solar incidence angles, so that the brightness temperature of the full
Moon decreases more slowly from the center to the limb than expected on
the basis of equilibrium temperatures and isotropic emission. Unfortunately
all the published lunar studies describe the 10\dmic\ atmospheric window
only: there is no available data in the 20\dmic\ window to give information
on the wavelength dependence of the beaming effect. Observations of beaming
at a variety of wavelengths were made for both Mercury and the Moon by
Murdock (1974), but these were disk-integrated measurements that are difficult
to compare with the disk-resolved Voyager data.
Lunar beaming has been successfully modelled as being a consequence
of local surface topography (e.g. Winter and Krupp (1971)). Sunlit depressions
receive radiation (scattered solar and re-radiated thermal) from the walls
around them as well as directly from the sun, and are thus warmer than
nearby elevated points. An observer at low phase angles will receive the
extra radiation from the warm depressions, whereas observations of the
same area at high phase angles will preferentially see the cooler elevations,
and shadowed regions that may be cooler still. Chapter 6 and Appendix
B discuss (and partially reproduce) these models, in an attempt to
explain the variations in spectrum shape with temperature that were described
in Chapter 4.
Measuring Beaming on the Galilean Satellites
There are two motivations in the current work for determining the anisotropy
of thermal emission from the Galilean satellites. The first is to compare
with the known lunar beaming, and with theoretical modelling (Chapter 6)
to see whether the beaming places any useful constraints on surface properties.
The second is to see if it is possible to use the knowledge of beaming
to remove the effects of changing viewing geometry from the IRIS data.
Because the Voyager IRIS coverage of the Galilean satellites is inadequate
to fully characterize the anisotropy of the thermal emission, this second
goal also requires comparison with the Moon to fill in some of the gaps.
The Saari et al (1972) lunar data refer only to a wavelength
of 11 microns, and thus give no information about the wavelength dependence
of the beaming. Hansen (1977), however, using a topographic thermal model
(see Chapter 6 and Appendix B), calculates
(disk-integrated) beaming at a range of wavelengths. He shows that wavelength
can be parameterized as the ratio $\lambda/\lambda_{max}$, where $\lambda_{max}$
is the wavelength of peak thermal emission from the planetary object at
zero phase. For the Saari et al observations, he gives this ratio
as about 1.2 (in his Fig. 5): for Ganymede and Callisto the wavelength
corresponding to this ratio is about 26 microns. This is the appropriate
wavelength of the IRIS observations to compare with the lunar data.
I measured beaming on the Galilean satellites by comparing overlapping
IRIS scans of a single region taken from different viewing geometries.
The temperature change between the two scans, when corrected for `real'
temperature changes due to the rotation of the body, gives a measure of
the directional dependence of the emission. I concentrated on measuring
variations in thermal emission with phase angle, as lunar beaming depends
mostly on this variable (Saari et al, 1972). To be detectable, temperature
variations due to beaming must be larger than those due to pointing uncertainties.
The Voyager 2 Ganymede data, having the highest resolution and best pointing
accuracy (after correction) of the icy satellite data sets, were thus used
for this purpose. Even here, the data is barely adequate to quantify the
beaming effects. I also made one measurement on Callisto for comparison,
though here the resolution is poorer still.
Table VII. Observations of Beaming on Ganymede and Callisto
|
Location
|
Phase
|
|
|
TE
|
26 mic m TB
|
|
|
Lat. |
Long. |
alpha1 |
alpha2 |
Local Temp. |
Rotional
$D$T |
Observed
dT |
Corrected
dT |
c X 103 |
Observed
dT |
Corrected
dT |
c X 103 |
Lunar 11mic m
c X 103 |
| G1 |
-20 |
190 |
34 |
44 |
135 |
+0.13 |
-2.0 |
-2.0 |
-1.47 |
-1.5 |
-1.5 |
-1.11 |
-0.79 |
| G2 |
-20 |
190 |
44 |
81 |
135 |
+0.03 |
-5.0 |
-5.0 |
-1.01 |
-3.0 |
-3.0 |
-0.60 |
-1.18 |
| G3 |
-30 |
150 |
44 |
59 |
122 |
-0.67 |
-3.0 |
-3.0 |
-1.38 |
-3.0 |
-2.5 |
-1.38 |
-1.20 |
| G4 |
-55 |
190 |
50 |
101 |
120 |
+0.13 |
-7.0 |
-7.0 |
-1.15 |
-6.0 |
-6.0 |
-0.98 |
- |
| G5 |
-60 |
160 |
48 |
66 |
107 |
-0.32 |
-4.0 |
-4.0 |
-1.81 |
-3.0 |
-2.5 |
-1.30 |
- |
| G6 |
-30 |
150 |
59 |
81 |
120 |
-0.70 |
-3.0 |
-3.0 |
-0.95 |
-2.0 |
-1.5 |
-0.57 |
-1.02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| C1 |
+35 |
10 |
50 |
79 |
137 |
-1.10 |
|
|
-3.0 |
-.073 |
|
|
|
See text for details. alpha1 and alpha2
are the two phase angles at which temperatures were compared to obtain
the thermal phase coefficients c.
In the southern hemisphere of the Voyager 2 region of Ganymede, I found
six instances of overlapping coverage of the same region at a pair of phase
angles. Results for these instances (G1--G6) are listed in Table VII, along
with the Callisto measurement (C1). For each instance, using plots showing
brightness temperature for each spectrum as a function of geographical
position, I drew isotherms by hand for each phase angle. I then recorded
the offset between the two sets of isotherms, corresponding to the temperature
change between the pair of observations. In each case the offset was in
the expected sense, with higher phase angle observations being cooler,
providing some confidence that I was observing a real effect. I determined
the offset for both 26\dmic\ TB, for comparison with
the 11\dmic\ lunar data, and for the wavelength-integrated TE.
For Ganymede, I corrected for the `real' cooling of the surface between
the observations, due to the satellite rotation (all the data comes from
afternoon regions), by reference to theoretical diurnal temperature profiles.
Direct inference of the afternoon cooling rate, from the observed temperature
distribution as a function of local time, is probably unreliable on Ganymede,
because of the quite strong perturbations due to local albedo variations.
At the time that I was doing this analysis, my best fit to the Ganymede
diurnal temperature profile was a single-layer thermal model with a thermal
inertia of 105 erg-cgs and an albedo of 0.3. I ran this model
for each latitude in Table VII to determine the expected surface cooling
during the time interval between the overlapping scans.
A problem with this approach is that this 1-layer model predicts a
diurnal temperature peak that is significantly longer after midday than
is observed on Ganymede. This means that the temperature is predicted to
be still rising slightly for locations G1, G2, and G3, while in reality
there was probably a slight cooling during the observations. Fortunately,
as Table VII shows, the rotational corrections are much smaller than the
observed phase-related reductions in brightness temperature so the effect
of this error is small. In the three cases where the thermal model predicted
a temperature rise, I applied no rotational correction (constant surface
temperature was assumed).
Subsequent thermal modelling (Chapter 7) gives an improved fit to the
Ganymede diurnal temperature profile, but I have not repeated the rotational
corrections because their small magnitude does not justify an improved
calculation.
On Callisto, where albedo variations are much smaller, I used the actual
observed afternoon cooling rate, deduced from the isotherm spacing, to
determine the expected surface cooling between the pair of observations.
I define a `thermal phase coefficient', c, as the fractional
change in temperature per degree of phase angle, so that for two values
of TE (or TB) at two phase angles
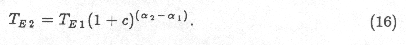
c is tabulated in Table VII. It varies by almost a factor of
two between the various cases. Table VII compares the 26\dmic\ c values
for cases G1, G2, G3, and G6, which are quite close to the thermal meridian,
with those for corresponding geometries at 11 microns on the Moon, derived
from both the observations of Saari et al Fig. 13, and the theoretical
model of Winter and Krupp, Fig. 9. It can be seen that there is no good
correspondence in the variations of c with viewing geometry between
the lunar and Ganymede data. This suggests, if the beaming on Ganymede
is similar to that on the Moon, that the twofold variability in c seen
on Ganymede is a result of observational error rather than a true dependence
on viewing geometry. Such large errors are not suprising considering the
pointing uncertainties and resolution of the data. The single value of
c
for Callisto is probably equally or more inaccurate. However, the Ganymede
and Callisto thermal phase coefficients are of the same magnitude (and
sign!) as those observed on the Moon, and are therefore probably real.
Possibility of Corrections for Beaming Effects
Because of the probable factor of two (at least) uncertainty in the
c values, and the limited range of geometries for which they are available,
I decided that an attempt to correct the Ganymede and Callisto effective
temperatures for viewing geometry would not be worthwhile. There would
be too much danger of overcorrecting and obtaining `corrected' temperatures
that were less accurate than the original values.
However the values of c that I obtain, close to 10-3,
allow an estimate of the temperature uncertainties introduced by the varying
viewing geometry. Saari et al (1972) Fig. 11 shows, for the Moon,
that `accurate' 11\dmic\ brightness temperatures (equal to the surface
equilibrium temperature) are obtained at phase angles between 45o
and 60o on the thermal meridian. From equation 15, using a
c value of 10-3, and an `accurate' phase angle of 50o,
a 120oK surface would appear to be at 122.4oK at
30o solar phase angle and 115.3oK at 90o
phase. The plots of surface temperature distributions presented in Chapter
5 will include uncertainties of this magnitude due to viewing geometry
variations.