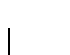Introduction to 1620 Geographos

The shapes of several Earth-crossing objects (ECOs) have now been inferred by delay-Doppler radar techniques ([Ostro 1993,Ostro et al., 1995a,Ostro et al., 1995b,Hudson and Ostro 1994,Hudson and Ostro 1995,Hudson and Ostro 1997]). They show that ECOs have irregular shapes, often resembling beat-up potatoes or even contact binaries. It is generally believed that these shapes are by-products of asteroid disruption events in the main belt and/or cratering events occurring after an ECO has been ejected from its immediate precursor. A few of these bodies, however, have such unusual shapes and surface features that we suspect an additional reshaping mechanism has been at work. As we will show, at least one ECO, 1620 Geographos, has the exterior characteristics, orbit, and rotation rate of an object which has been significantly manipulated by planetary tidal forces.

1620 Geographos is an S-class asteroid with a mean diameter slightly over 3 km. It was observed with the Goldstone 2.52-cm (8510-MHz) radar from August 28 through September 2, 1994 when the object was within 0.0333 AU of Earth ([Ostro et al., 1995a,Ostro et al., 1996]). A delay-Doppler image of Geographos's pole-on silhouette (Fig. 1) showed it to have more exact dimensions of 5.11 x 1.85 km ( 2.76 x 1.0, normalized), making it the most elongated object yet found in the solar system ([Ostro et al., 1995a,Ostro et al., 1996]). In addition, Geographos's rotation period (P = 5.22 h) is short enough that loose material is scarcely bound near the ends of the body ([Burns 1975]). 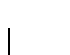For reference, Geographos would begin to shed mass for $P \lesssim 4$ h if its bulk density was 2.0 g ${\rm cm}^{-3}$ (Harris 1996; Richardson et al. 1998).

fig1

Geographos's elongated axis ratio was unusual enough that Solem and Hills (1996) first hypothesized it may not be a consequence of collisions. Instead, they speculated it could be a by-product of planetary tidal forces, which kneaded the body into a new configuration during an encounter with Earth.

To test their hypothesis, they employed a numerical N-body code to track the evolution of non-rotating strengthless spherical aggregates making close slow passes by the Earth. Some of their test cases showed that tidal forces stretch spherical progenitors into cigar-like figures as long or longer than the actual dimensions of Geographos. Since ECOs undergo close encounters with Earth (and Venus) with some frequency (Bottke et al., 1994), Solem and Hills (1996) postulated that other ECOs may have comparable elongations.

Though Geographos's elongation is provocative, it is, by itself, an inadequate means of determining whether the asteroid has been modified by tidal forces. To really make the case that 1620 Geographos is a tidally distorted object, several questions must be answered:

A.

Is Geographos's internal structure (or that of any other ECO) weak enough to allow tidal forces to pull it apart?

B.

How likely is it that Geographos ever made a close slow encounter with a large terrestrial planet like Earth or Venus?

C.

Can tidal forces reshape an ECO into a Geographos-like silhouette (not just an asymmetrical elongated figure) and reproduce its spin rate?

D.

If so, how often do such events occur?

E.

Is Geographos a singular case, or have other ECOs undergone comparable distortion?

In the following sections, we will address each of these questions in turn. Our primary tool to investigate these issues is the N-body code of Richardson et al. (1998), more advanced than the code of Solem and Hills (1996) and capable of determining the ultimate shape and rotation of our progenitors. By applying a reasonable set of ECO starting conditions, we will show that Geographos-type shapes and spins are a natural consequence of tidal disruption. The results discussed here are based on the extensive parameter space surveys completed for Richardson et al. (1998).